That is a Graph Problem!

English: A 4-node graph for illustrating concepts in transportation geography and network science. (Photo credit: Wikipedia)

Recently at the Data Modeling Zone conference I was asked how to identify a problem as something that should be solved with graph tools.

The difficulty, I think, for data modelers is that many of us with a relational background tend to think about the relationships of our data structures.

This table is related to this other table with a one-to-one relationship, or one-to-many, or many-to-one, or even many-to-many relationship.

There are whole books devoted to discussing how to create relational data models that support these relationships.

I wrote a little about Graph fundamentals here: http://bit.ly/GraphFundamentals, but applying these atomic definitions to a real world problem can be a bit of a stretch.

There are, however, a few words to key in on.

Path:

What is the path that a customer takes through our store?

English: Precedence graph Based on :Image:Directed.svg (Photo credit: Wikipedia)

This is clearly a graph type problem. It could also be a time-series type problem. If you want to look at an individual you would see one thing. If you take large sampling of your customer base and load that into a network visualization tool like Gephi then you may learn some new things, and gain additional insight into the layout of your store.

A path is about more than just the relationship between two things. It is about the relationship of many things, and how something (like a customer, or some data ) flows through the graph.

Learning the optimal path through a set of obstacles would require some iterative path analysis work.

These types of path questions are common in the human resource domain from the perspective of career path.

A segment of a social network (Photo credit: Wikipedia)

People:

Social Network Analysis is one of the practical applications of graph theory.

Milgrams experiments are key touch-points that are commonly mentioned trying to understand the degrees of separation of two items. How often do people speak to one another? Does Ann talk to Bob, then speak to Charlie all the time?

If Ann says something positive about your brand, will Bob and Charlie both like your product?

If Ann says something negative will your stock price go down?

Who is talking about your products and who is listening to them?

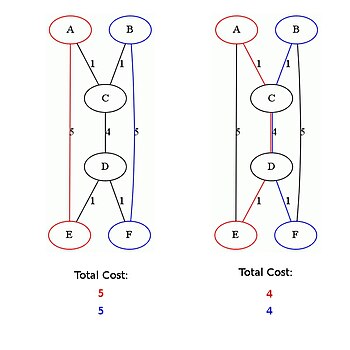English: Example of the Shared Shortest Path Problem (Photo credit: Wikipedia)

Data Itself:

My thoughts about understanding how data movement, and data structures themselves can be thought of as a graph, I have written about previously: http://bit.ly/DataStructureGraph

Some other terms in similar context are Data Lineage, and Data Pipeline.

How does data flow through your organization?
How does it flow into your organization?

How does it flow out of your organization?

Once in your organization how many systems does the same data flow into and out of without enrichment?

Does this data really need to go into those systems?


Movement:

How does a thing (Package, Product, Person, or Participant) move that your company interacts with? Rarely does it move from only one place to another.

Each step in the thing moving from one place to another is part of a path mentioned above.

You may think that a product moving from a shelf, to a box, then on to a truck for delivery to a customer can all be handled by individual applications. This is entirely possible. the value to doing graph analysis is new insight into existing data.


I would never suggest that Graph Analysis or Network Science is the only way to look at a problem.
I would suggest hat these tools can provide new or unique insight into the problems where businesses are trying to solve problems related to :Paths, people, Data, or Movement.

After all, Data Science  applies a fresh perspective on our existing world.

We should all be trying to achieve more with our data.

Sentiment Text ETL.

English: Robert Plutchik's Wheel of Emotions (Photo credit: Wikipedia)

I attended a presentation by Bill Inmon where he spoke of the value to various businesses of his product called TextualETL.

There was a question in the audience about trying some of these text techniques ourselves, is there anything he could teach us.

The answer was less that satisfying to a do it yourself-er like some of us in the audience.

I have had some reason to do basic sentiment analysis at work recently and I was really looking forward to his talk.

Since the question was raised about how to get started in this area without totally going overboard, I will share some of my experiences.

I use R and SQL for the majority of my work, so the sentiment work will be some basic R code.

If there is some interest, please post a comment, and I will add this to my github for sharing.

Here is a small sample for doing sentiment:

library(syuzhet)
# Get sentiment on the comments of the source data set
sentiment_data <- get_nrc_sentiment(as.character(source_data_frame$Comments))
# Transpose rows to columns
transposed_sentiment_data<-data.frame(t(sentiment_data))
# Summarize the data so we have a single row per sentiment.
transposed_sentiment_data_summary <- data.frame(rowSums(td[1:length(transposed_sentiment_data)]))
# change the name of the result set
names(transposed_sentiment_data_summary)[1] <- "count"
transposed_sentiment_data_summary <- cbind("sentiment" = rownames(transposed_sentiment_data_summary), transposed_sentiment_data_summary)
rownames(transposed_sentiment_data_summary) <- NULL
# only get the emotional data into the subset.
subset_sentiment_data<-transposed_sentiment_data_summary[1:8,]
# display a quick plot
qplot(sentiment, data=subset_sentiment_data, weight=count,fill=sentiment) +ggtitle(plot_title)
# display a plot that is just positive or negative data.
qplot(sentiment, data=transposed_sentiment_data_summary[9:10,],weight=count,fill=sentiment)+ggtitle('Positive/Negative')


So long as your source data set has some business key stored in it, this data frame can be written out to a data base (I use snowflake), as a staging table, that is then transformed to a Fact table.

I created a small dimension table for sentiment like this:

INSERT INTO dim_sentiment VALUES
(1,'ANGER'),
(2,'ANTICIPATION'),
(3,'DISGUST'),
(4,'FEAR'),
(5,'JOY'),
(6,'NEGATIVE'),
(7,'POSITIVE'),
(8,'SADNESS'),
(9,'SURPRISE'),
(10,'TRUST');


These are the sentiments available using the get_nrc_sentiment() function from the syuzhet package.

There are some much more sophisticated techniques that could be done with R and text analysis, but this is just a small taste of what can be done.

As a suggestion, I could see how doing some Topic Modeling of your comment data could lead to new dimensions you would want to incorporate into your data warehouse. Another thought is to record the timestamps of comments mad that are transcribed from a customer service call.

Does the sentiment change over time of the customer that is being helped? You would hope so.

Which one of your customer service agent consistently has the largest swing from negative to positive?
Don't know the answer to this question?

Maybe you should think about Text analytics.


Translating Textual data into data that can be used in a data warehouse is only one way of leveraging text data, but if you have powerful self service tools like Tableau, Looker, or Microstrategy, having your data in this structure makes it easy for some quick analysis on what people are thinking in the feedback they are giving to you.

Always,  when doing this type of text analysis, ensure that you have some type of business key that associates the voice of this customer to the summation of what they are saying.

Narrowing down the positive or negative comments can be invaluable for finding the needle in the haystack for the feedback you are interested in.

Related articles

• What Facebook Reactions Mean for Brands
• Data is the name of the game, as Intel Capital puts $60M in 15 startups, $566M in 2017 overall

Equally Incremented Sequential Numbers

I have been studying an interesting pattern of numbers recently. 

It is related to a comment I have heard said repeatedly by statisticians, that seems like it should not be true. 

The comment is: “If you play the lottery why not just pick the number 1,2,3,4,5 or 2,3,4,5,6? They are just as likely to show up as any other number.” 

However, if they are just as likely to show up why do they so seldom appear in the random number generator that is the lottery? 

Let us see if we can determine why this is the case. 

But first we must create some narrow definitions, and a formula. 

The above sequence fits the definition of five consecutive numbers equally incremented by some number. In this case the number one. 

When defining the odds for winning the lottery the total number of possibilities is referenced. Your odds of winning are 1/(N choose K). The number you have chosen must match the 1 set of numbers that come out of the drawing based on the selection of K numbers form N possibilities.

Do equally incremented sequential numbers appear to behave differently? To be able to count how many equally incremented sequential number sets of length K could be selected from a set of size N the mathematical notation becomes: 

N-S(K-1)

In human readable terms this yields the total number of equally incremented sets of K items from the set size N, with a sequential increment of S.

This expression gives the results it does based on the following: 

By the nature of consecutive numbers the maximum first number in the set produced will be the product of the increment and the length of the selection set minus one. 

Since these are consecutive numbers this maximum first number is also the total number of all equally incremented consecutive numbers that can be drawn from the set of size N.

Let us do a small demonstration. 

Setting N to 8, and K to 3 the total number of selections we could get out of this combination is 8 choose 3  which is 56.  To get the total number of possible equally incremented sequential numbers we must increment count the number numbers produced by each increment of S

The colors represent the counts.

Purple: 8-1(3-1) = 6 {(1,2,3)(2,3,4)(3,4,5)(4,5,6)(5,6,7)(6,7,8)}

Green : 8-2(3-1) = 4 {(1,3,5)(2,4,6)(3,5,7)(4,6,8)}

Blue  : 8-3(3-1)  = 2 {(1,4,7)(2,5,8)}

 

 

The summation is: 

The sum of these individual calculations is 12.

Now that we have this number the question we want to ask is: 

What is the probability that 3 numbers chosen from the set of 8 will be equally incremented sequential numbers ? 

The probability is 12/56. 

What is the probability that 3 numbers chosen from the set of 8 will not be equally incremented sequential numbers ?

44/56. 

Reducing the results, we have 3/14, and 11/14 respectively.

There are 11 to 3 odds against choosing three equally incremented sequential numbers from a set of 8 numbers. 

This is one way of determining the odds of equally incremented sequential numbered sets of numbers coming out of a random number generator like a lottery drawing.

There are a few other use cases for this formula related to path length calculations for graphs that I will continue to research. More to come on this interesting formula.